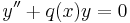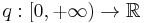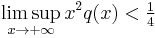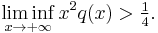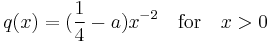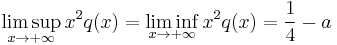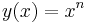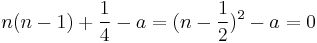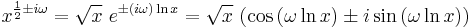Kneser theorem
In mathematics, in the field of ordinary differential equations, the Kneser theorem, named after Adolf Kneser, provides criteria to decide whether a differential equation is oscillating or not.
Contents |
Statement of the theorem
Consider an ordinary linear homogenous differential equation of the form
with
continuous. We say this equation is oscillating if it has a solution y with infinitely many zeros, and non-oscillating otherwise.
The theorem states[1] that the equation is non-oscillating if
and oscillating if
Example
To illustrate the theorem consider
where  is real and non-zero. According to the theorem, solutions will be oscillating or not depending on whether
is real and non-zero. According to the theorem, solutions will be oscillating or not depending on whether  is positive (non-oscillating) or negative (oscillating) because
is positive (non-oscillating) or negative (oscillating) because
To find the solutions for this choice of 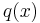 , and verify the theorem for this example, substitute the 'ansatz'
, and verify the theorem for this example, substitute the 'ansatz'
which gives
This means that (for non-zero  ) the general solution is
) the general solution is
where  and
and  are arbitrary constants.
are arbitrary constants.
It is not hard to see that for positive  the solutions do not oscillate while for negative
the solutions do not oscillate while for negative 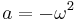 the identity
the identity
shows that they do.
Extensions
There are many extensions to this result. For a recent account see[2].
References
- ^ Teschl, Gerald (2011). Ordinary Differential Equations and Dynamical Systems. American Mathematical Society. http://www.mat.univie.ac.at/~gerald/ftp/book-ode/.
- ^ Helge Krüger and Gerald Teschl, Effective Prüfer angles and relative oscillation criteria, J. Diff. Eq. 245 (2008), 3823-3848 [1]